generalized coordinates
The Basics
Generalized coordinates are a minimal set of independent parameters that completely describe a robot's configuration—its exact shape and pose. For most robots, these are simply the joint angles.
If you know all generalized coordinates, you know precisely what the robot looks like at that moment.
Simple Concept
Instead of tracking:
- Position of link 1
- Position of link 2
- Position of link 3
- Position of gripper
- Orientation of each part
- ... (hundreds of data points)
Just specify:
- Joint 1 angle: 45°
- Joint 2 angle: 30°
- Joint 3 angle: 60°
That's it. Everything else follows from these three numbers.
q = [θ₁, θ₂, θ₃] ← Generalized coordinates
= [45°, 30°, 60°]
From this alone, you can calculate:
- Position of every point on the robot
- Orientation of every link
- Center of mass
- Where the gripper is
Why "Generalized"?
"Generalized" means:
- Not specific to any particular representation
- Works for any robot structure
- Minimal set (no redundant information)
- Independent (each one contributes unique information)
"Coordinates" means:
- They parameterize (describe) the configuration
- Like x, y, z coordinates but for robot shape
For Different Robot Types
6-DOF Arm
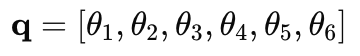
Six joint angles = complete configuration
3-DOF Cartesian Robot
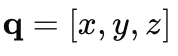
Three linear positions = complete configuration
Mobile Manipulator (Robot + Arm)
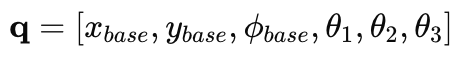
Base position + base orientation + 3 arm angles
Real-World Example
Pick-and-place robot arm:
Current configuration:
q = [0°, 90°, 45°, 180°]
This tells you:
- Base is rotated 0° (pointing straight)
- Shoulder bent at 90° (arm horizontal)
- Elbow bent at 45° (forearm angled up)
- Wrist rotated 180° (gripper upside down)
You can instantly visualize the exact pose.
Mathematical Notation
Generalized coordinates are typically written as:
Connection to Kinematics
Forward kinematics uses generalized coordinates:
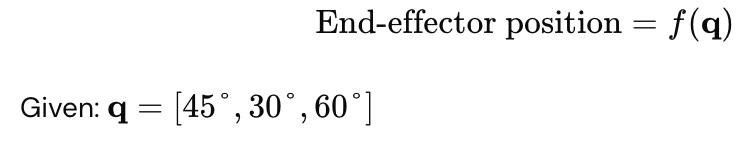
Calculate: Where is the gripper in 3D space?
Input (generalized coordinates)
↓
q = [45°, 30°, 60°]
↓
Forward kinematics (f function)
↓
Output: Gripper at (x=0.5m, y=0.3m, z=0.8m)
Why Generalized Coordinates Matter
Benefit | Explanation |
Minimal description | Only what's necessary, nothing redundant |
Easy storage | Store robot trajectory as array of numbers |
Fast computation | Fewer parameters = faster calculations |
Control simplicity | Command individual joints, not every point |
Universal framework | Works for any robot structure |
Practical Applications
Motion Recording
Recorded trajectory (4 waypoints):
Waypoint 1: q = [0°, 90°, 45°, 180°]
Waypoint 2: q = [15°, 85°, 50°, 175°]
Waypoint 3: q = [30°, 80°, 55°, 170°]
Waypoint 4: q = [45°, 75°, 60°, 165°]
Replay by commanding each q sequentially
Simulation
Virtual robot position at time t:
q(t) = [θ₁(t), θ₂(t), θ₃(t)]
Calculate any property from q(t):
- Velocity: dq/dt
- Acceleration: d²q/dt²
- Position: f(q(t))
Control Algorithm
Controller sends:
"Move to q = [30°, 60°, 45°]"
Each motor receives its target:
- Motor 1: Go to 30°
- Motor 2: Go to 60°
- Motor 3: Go to 45°
Independence is Key
Generalized coordinates must be independent:
✓ Valid: $[45°, 30°, 60°]$ — each angle is independent
✗ Invalid: $[45°, 30°, 30° × 2]$ — last angle depends on second angle (redundant)
Constraints and Reduced Coordinates
Sometimes constraints reduce generalized coordinates:
Example: Wheeled robot on ground
Full position: (x, y, z, pitch, roll, yaw) — 6 parameters
Constraints: z = 0 (on ground), pitch = 0, roll = 0
Generalized coordinates: q = [x, y, yaw] — only 3 parameters
The constraint removes 3 redundant parameters.
Configuration Space (q-space)
Generalized coordinates define configuration space:
3-DOF robot:
Configuration space = 3D space
Each point (q₁, q₂, q₃) is one possible robot pose
2-DOF robot:
Configuration space = 2D plane
Each point (q₁, q₂) is one configuration
Key Comparison
Aspect | Details |
Cartesian coordinates | Describe position in 3D space (x, y, z) |
Joint angles | Describe robot internal configuration (θ₁, θ₂, θ₃) |
Generalized coordinates | The general term for any minimal parametrization |
For most robots: generalized coordinates = joint angles
Key Takeaway
Generalized coordinates are the "DNA of robot pose"—a minimal, independent set of parameters that completely describes the robot's configuration. For most robots, these are simply joint angles. Knowing all generalized coordinates lets you reconstruct everything about the robot's shape, position, and orientation. This is fundamental to robot control, kinematics, dynamics, and motion planning.